Courbes de Lissajous
Comparaison des fréquences
Si on applique aux plaques de déviation horizontale et verticale d'un oscilloscope deux
tensions sinusoidales de fréquence f1 et f2 tel que :
X= a. sin (2.pi.f1.t)
Y=a. sin (2.pi.f2.t)
On observe sur l'écran des courbes fermées , fixes , lorsque le rapport des fréquences
f1 et f2 des deux vibrations est égal au rapport de deux nombres
entiers m et n : f2 / f1 = m / n
Ces courbes, inscrites dans un rectangle de cotés a et b , sont appelées courbes de
Lissajous. Le nombre des points de tangence sur les côtés horizontaux et verticaux
détermine le rapport des fréquences des deux vibrations.

Exemple f2 / f1 = 7 / 3

Si, faisant varier f2 , le rapport f2 / f1 =m/n
diffère peu du rapport de deux nombres entiers, les courbes de Lissajous se déforment
périodiquement à la fréquence F = f1 .m/n - f2
Pour observer ces courbes de Lissajous , il faut disposer d'un oscilloscope à deux
voies, et appliquer à l'aide de deux générateurs B.F les deux tensions x et Y sur
chacune des voies et supprimer le balayage horizontal de l'oscilloscope position XY
Exemples de figures
f2 / f1 = 2 / 3
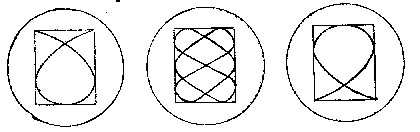
f2 / f1 = 1 ( Ellipses à déphasage continuement variable )
f2 / f1 = 2
f2 / f1 = 3
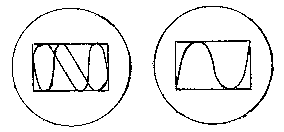
Vous pouvez essayer de reproduire ces courbes.
Retour à la page Courbes de Lissajous